Kısaca hatırlayacak olursak, biz istatistik testleri iki gruba ayırmıştık bunlardan ilki parametrik, diğeri ise non-parametrik istatistiklerdi. Bunların birbirinden farkı, parametrik istatistikler daha az hata barındıran daha güçlü kararlardı, ama sayıtılar sağlanmadığı zaman bunların non-parametriklerine başvurabiliyorduk. İlk konuşacağımız test, Bağımsız Gruplar T- testinin non parametrik testi olan Mann Whitney- U Testi olacak.
Mann Whitney U Testi
Mann Whitney- U Testi
Bu testte amaç iki ilişkisiz örneklemden elde edilen puanların birbirinden anlamlı şekilde farklılık gösterip göstermediğini test eder. Bu test bağımsız örneklemler için uygulanan t testin non- parametrik halidir. Bu test bağımsız gruplar için t testi sayıltısının karşılanmadığı durumlarda kullanılır. Bu testin sayıltıları;
- Bağımlı değişken en az sıralama düzeyinde olması gerekiyor.
- Gözlemlerin birbirinden bağımsız olması gerekiyor.
Şimdi bir problem cümlesi üzerinden testimi yapmaya başlayalım.
Problem Cümlesi; Bir araştırmacı 46 kişilik bir grubun yarısını sınav kaygılarını azaltmaya yönelik 5 haftalık bir terapi yöntemi uyguluyor. Grubun diğer yarısına ise herhangi bir yöntem uygulamıyor. Bu beş hafta sonucunda terapi yöntemi uygulanan grup ile uygulanmayan grubun kaygı düzeyleri açısından anlamlı bir farklılık var mıdır?
46 kişi ikiye bölersek 23 kişi olarak ayrılacak- burada eşit olma zorunluluğu yok ama eşit olmasını tercih ederiz-. Test için 23 kişi ile normal dağılım sağlanamayacağı var sayılırsa non- parametrik test yapıyoruz. Aslında 30 sayısının üstüne çıktığımızda da normal dağılım göstereceği anlamına gelmiyor. Bunun için normallik testleri ile normal dağılım gösterip göstermediğine bakıyoruz.
Normallik testi için spss veri setlerimizi uygun girdikten sonra Anayze—> Descriptive Statistics—> Explore diyoruz
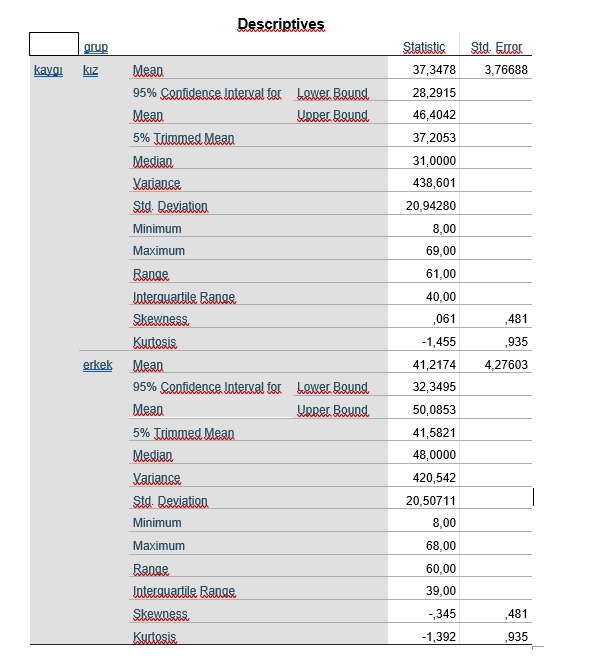
Tanımlayıcı istatistik tablomuza göz attığımızda ortalama ile medyan arasında oldukça fark var “skewness”, “kurtosis” değerleri istenilen değerler değil ve son olarak histogram grafiğimize baktığımızda;
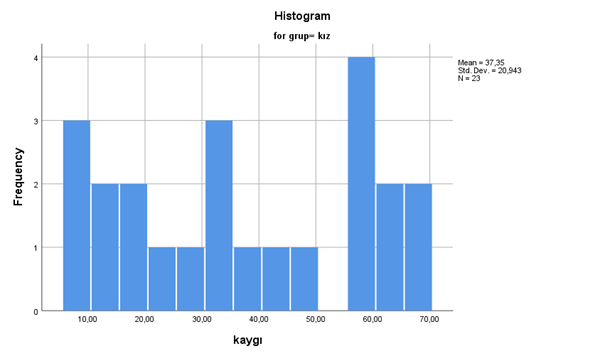
Normal dağılım göstermediğini görmekteyiz. Artık non-parametrik test olacağı kesinleştiği için ve kız ve erkek olmak üzere iki bağımsız grup olması nedeniyle, Mann Whitney U Testini yapmaya geçebiliriz. Analyze—> Nonparametric Tests—>Legacy Dialogs—>2 İndependent samples … diyoruz
Daha sonra gelen pencerede kaygıyı “Test Variable List” kutusuna Grup değişkenini ise “Grouping Variable” kutusuna atıp grupları 1 (kız), 2 (erkek) diye tanımlıyoruz. Alt tarafta “Test Type” kısmı otomatik Mann- Whitney U olarak işaretli gelecektir. Daha sonra OK diyoruz ve outputları inceliyoruz.
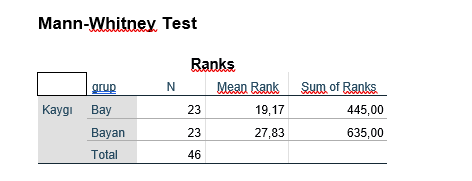
Her zaman olduğu gibi ilk başta bir takım betimleyici istatistikler veriliyor bunlara bakacak olursak. 23 bay 23 bayan olmak üzere toplan 46 kişi var. Bayların ortalaması 19, 17 iken, bayanların ortalaması 27, 83 olduğu görülmektedir. Buradaki farkın anlamlılığına bakmak için, karar istatistiklerine baktığımızda;
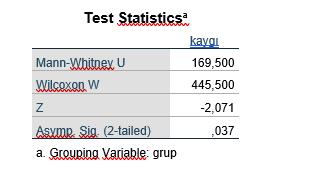
Mann Whitney U değeri: 169,5 ve buna ilişkin manidarlık düzeyi ise .03 olarak görülmektedir. Bu iki grup arasında manidar bir fark olduğunu göstermektedir. Bu farkın bayanların sıra ortalaması daha yüksek olduğu için bayanların lehinde diyebiliriz. Verileri makalede veya tezde ifade ederken aşağıdaki tabloyu kullanabiliriz.
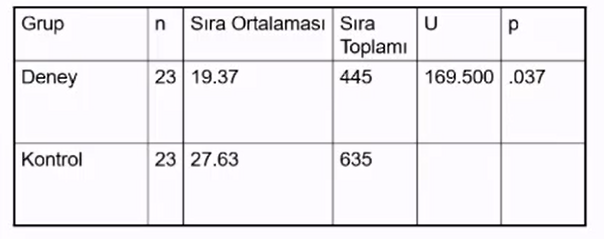
Man Whitney U testi sonuçlarına baktığımızda 5 haftalık verilen terapi yönteminden sonra gruplar arasında anlamlı fark görülmüştür (U= 169.500, P<.05). Sıra ortalamaları dikkate alındığında terapi uygulanan grubun kaygı düzeyleri, kontrol grubuna göre daha düşük olduğu görülmüştür. (19.37<27.63)
