Kruskal Wallis Test
Amaç
İki ya da daha fazla örneklem ortalamasının anlamlı farklılık gösterip göstermediğini test eder. Tek yönlü varyans analizinin (One-Way ANOVA ) non-parametrik halidir. Anovanın sayıltıları karşılanmaz ise bu testi yapmamız gerekecektir.
Sayıltılarına bakacak olursak;
- Bağımlı değişken en az sıralama düzeyinde olmalıdır.
- Gözlemler birbirinden bağımsız olmalıdır.
Problem Cümlesi
İlköğretim düzeyindeki bir grup öğrencinin problem çözme becerilerini geliştirmeye yönelik 3 farklı eğitim programının etkililiği araştırılıyor. Öğrencilerin problem çözme becerisi puanları alınan eğitime göre anlamlı farklılık göstermekte midir?
Şekillinde bir durumumum olsun. Burada 3 farklı bir grup var ve problem çözme becerileri arasında fark var mı bunu görmek istiyoruz. 2 den fazla grup olması ve grupların bir birinden bağımsız olması varsayımı ile Kruskal Wallis testini uygulayabiliriz.
SPSS Programına uygun şekilde veri setlerini girdikten sonra
Betimsel istatistikleri görmek istersek Explore bize yardımcı olacaktır. Bunun için Analyze—>Descriptive Statistics—> Explore—> Dependent List kısmına Grup, Factor list Kısmına Puan değişkenlerini atayıp Statistics kısmından outliers lara bakalım, plots kısmından ise Hstogram seçip, Normality Plots with Tests’ i tıklayalım.
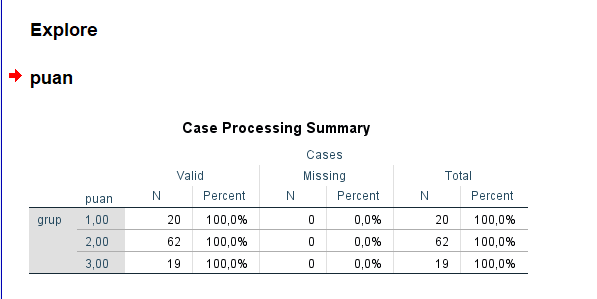
Bu tabloya baktığımızda 1. Grupta 20, 2. Grupta 62 ve 3. Grupta 19 kişi görülmektedir. Burada gruplardan bazıları 30 un altına düştüğü için normallik beklentisi düşmektedir. Bu tip yapılarda genellikle varyanslarda problem çıkar, grup sayıları ciddi oranda farklılaşıyorsa varyansların homojenliği risk altına girebilir.
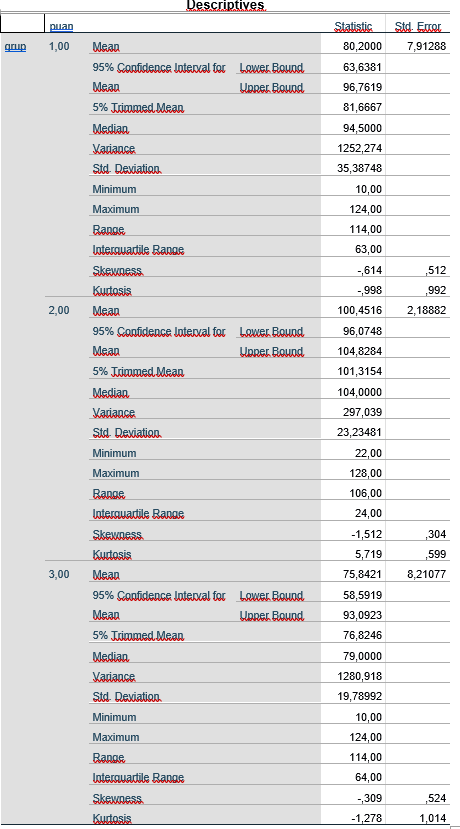
Grupların standart sapmalarına baktığımızda 1. grubun standart sapması 35, 2. Grubun standart sapması 23, 3. Grubun standart sapması ise 19 olarak görülmektedir. Bir farklılaşma işaretleri var burada, muhtemelen buna ANOVA yapsaydık ve varyanslar homojen mi deseydik hayır diyecekti.

Normallik testine baktığımızda 1. Grubun normallikten manidar derecede sapma yaşandığını (p=.039) yani normal dağılım göstermediğini görebiliyoruz. 2. Ve 3. Grubun ise Normal dağılım gösterdiğini görüyoruz. Kruskal Wallis Testimizi yapmak için, Anlyze—> Non Parametrik Tests—> Legacy Dialogs—> K independent Sampless.. diyoruz.
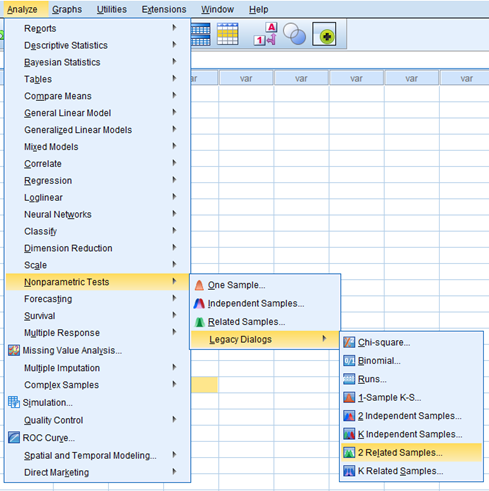
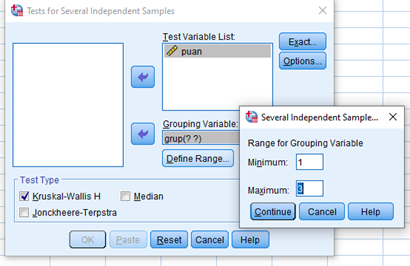
Daha sonra gelen ekranda Test Variable List kutusuna” puan”, Group Variables Kutusuna “grup” değişkenini atıyoruz, define gruptan 1 ile 3 arasındaki grupları karşılaştır diyoruz ve Options kısmından discriptives tıklayıp OK diyoruz.
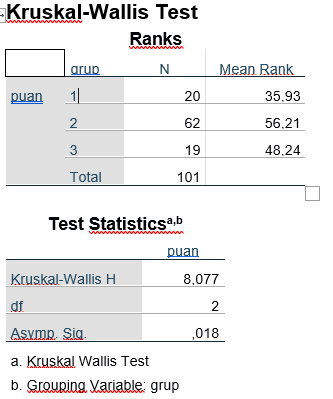
Test sonuçlarıan baktığımızda ( p= .018) anlamlı bir farklılık olduğunu görüyoruz. Gruplardan en az bir tanesinin ortalaması diğerlerinden farklıdır diyebiliriz. Kimin kimden farklı olduğunu bulmak için (Anova yapmış olsaydık post Hoc test yapmıştık ama burada yapamıyoruz) burada yapmamız gereken 2’li grupları karşılaştırmamız lazım bunun için Mann Withney U testi yapmamız gerekiyor. Yani 1. grup ile 2. grubu 1, grup ile 3. ve 2. Grup ile 3. grup karşılaştırmalarını yapmamız gerekmektedir. Yani 3 tane Man Withney U testi yapmamız lazım, ilk önce 1 ve 2. Grubu karşılaştıralım bunun için Anlyze—> Non Parametric Tests—> LegacyDialogs—> 2 independent Sampless diyoruz ve öncelikle 1 ve 2. Grubu karşılaştırıyouz.
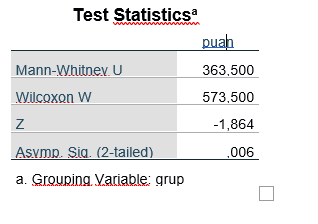
Görüldüğü üzere 1 ve 2. Grup arasında anlamlı bir farklılık görülmektedir. (p=0.006). şimdi ise yine bir mann Withney U testi yaparak 1 ve 3. Grubu karşılaştıralım.
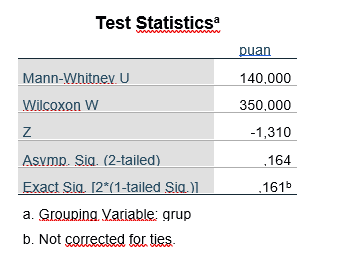
Görüldüğü üzere 1 ve 3. Grup arasında anlamlı bir farklılık görülmemektedir. (p=0.161). Şimdi ise yine bir Mann Withney U testi yaparak 2 ve 3. Grubu karşılaştıralım
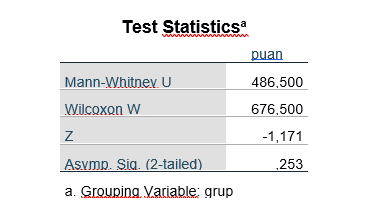
Görüldüğü üzere 12 ve 3. Grup arasında anlamlı bir farklılık görülmemektedir. (p=0.161). Buradan sadece 1 ve 2. Grup arasında anlamlı bir farklılık görülmektedir. Sonuçlarımızı tablolaştıracak olursak (Standart bir Kruskal Wallis tablosu sanırım yok )
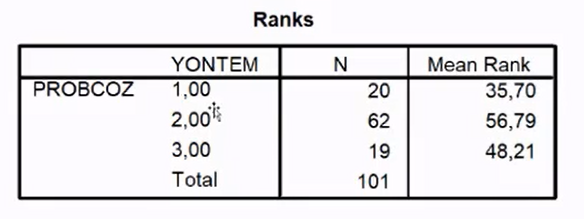
Yorumumuzu yapacak olursak; Analiz sonuçlarına göre, öğrencilerin problem çözme becerileri testinden aldıkları puanların, aldıkları eğitime göre farklılaştığı görülmektedir (X2 =8.05, p<.05). Grupların sıra ortalamaları dikkate alındığında eğitim sonrasında problem çözme becerisine 2. Eğitime katılanların en yüksek olduğu görülmektedir.
II. YOL
Kruskall Wallis Testini SPSS 25. Üzerinden farklı bir yolla daha yapabiliriz. Yani ayrı ayrı Mann Whitney U testi yapmadan tek bir testte yapabiliriz. Şimdi buna bir göz atalım. Veri seti girişinde grup değişkenini nominal yaptığımızı kontrol edelim. Daha sonra Analyze–>< Nonparametric Tests–> İndependent Samples diyoruz e çıkan ekranda objective kısmında tanımlamaları otomatik yapmasını istiyoruz. Fields’ i tıklayıp
Puan değişkenini Test Fields Kısmına, Grup kutusuna da grup değişkenini atıyorum
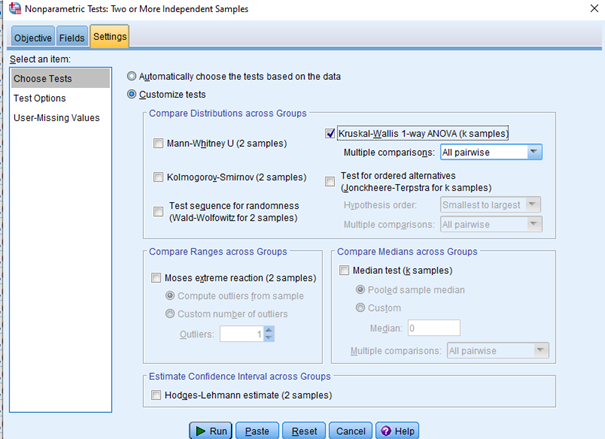
Daha sonra “Settings” tıklayıp customize tests’ i aktif hale getirip altta çıkan seçeneklerde Kruskal- Wallis 1 -way ANOVA (k Samples) i tıklıyoruz All pairwise seçeneği ile 3 grubun karşılaştırmasını aynı anda yapabiliyoruz.
SPSS bize tabloyu yorumlayıp veriyor ama biz daha fazlasını istiyoruz.

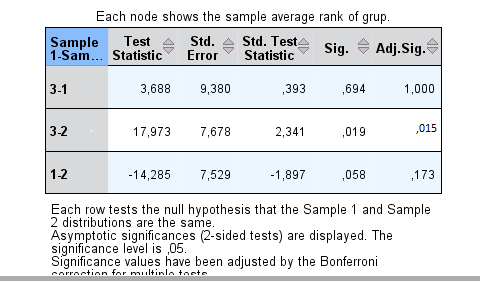
Çıkan tablonun üzerine çift tıkladığımızda aşağıdaki gibi verileri görebiliriz.
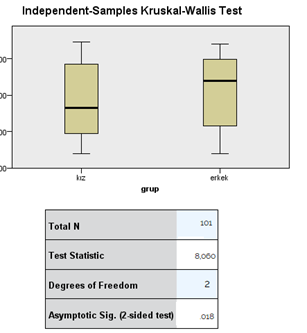
Burada görüldüğü gibi yokluk hipotezi reddedilebilir, yani puanlardan en az bir tanesi diğerlerinden farklıdır diyebiliriz. Bu farkın hangi grup lehine olduğunu görmek için en son çıkan sayfada alt kısımdaki View sekmesinde “Pairwise Comparisons” tıkladığımızda alttaki gibi grupları birbiri ile karşılaştırdığını görmekteyiz.