Bu tür testlerde örneklemlerin bir birinden bağımsız olması gerekiyor. Biraz daha açacak olursak iki grubun (kadın- erkek, evli-bekar, deney-kontrol grubu, vb), ortalamaları karşılaştırılarak, aradaki farkın rastlantısal mı, yoksa istatistiksel olarak anlamlı mı olduğuna karar vermek istendiğinde “Bağımsız Gruplar t-testi” kullanılır. Bu noktada yapacağımız hipotez testimizde bağımlı ve bağımsız örneklemler belirlenmeli, bağımsız örneklemlerde grupların bağımsız olması beklenmektedir.
Bağımlı gruplar için T- Testi ise aynı örneklem üzerinde tekrarlı ölçümler yapma diyebiliriz. örneğin Deney grubuna ön- test ve son- testi yapıyorsak bu bağımlı gruplar , deney ve kontrol grubuna ön test yapıyorsak ise bağımsız gruplar diyoruz. önceki bilgilerimizi de hatırlama adına araştırma sorumuzu oluşturacak olursak
Bağımsız Gruplar İçin Araştırma Sorusu : Deney ile kontrol grubunun ön test puanları arasında fark var mıdır?
Bağımlı Gruplar İçin Araştırma Sorusu : Kontrol grubunun ön test ile son test puanları arasında fark var mıdır? şeklinde olacaktır. Biz bu yazımızda Bağımsız Gruplar İçin T-Testi Hakkında konuşacağız.
Bu noktada bizlerin ilk yapacağı öncelikle grup sayımıza bakacağız. Çünkü bu sayılara göre yapacağımız testler farklılık gösterecektir. Örneğin deney ile kontrol grubu karşılaştırılıyorsa burada 2 grup var diyeceğiz. Ama bu gruplara bir üçüncü grup eklersek, diyelim ki izleme grubu eklemiş olalım o zaman yapacağımız testler de farklılaşacaktır. Daha sonra özelliklere bakacağız, Yani parametrik mi?, non- parametrik mi ?, bağımlı- bağımsız gruplar mı gibi.
Örneğin ; Kırsal kesimde yaşayan öğrenciler ile kentlerde yaşayan öğrencilerin covid-19 sürecinde öğrenme kayıpları var mı? şeklinde bir soruyu ele aldığımızda bu araştırma sorusu için SAYILTILARIMIZ’ a bakıyoruz
- Gruplar ilişkisiz mi ilişkili mi? ; burada kırsal ve kent olduğu için ilişkisiz (Bağımsız)
- Bağımlı değişkene ilişkin ölçümler her zaman iki grupta da normal mi? Yani hem kırsal hem de kent için normal dağılım gösteriyor mu? Bu genelde yanlış anlaşılıyor. Birinin normal dağılımı yeterliymiş gibi bir algı var. Her iki grup için de ayrı ayrı bakmamız gerekiyor.
- Bağımlı değişkene ait ölçümlerin en az eşit aralıklı veya oranlı olması lazım, sıralama ve sınıflama ölçeği ile bağımsız gruplar t- testi yapamayız. Bildiğiniz gibi sınıflama (Kadın- erkek, evli- bekar vb. ) ve sıralama (öğrenim durumu, ) ölçekleri ile matematiksel işlemler yapamayız. sadece frekans, yüzde, gibi değerlere bakabiliriz
- Her iki grubun varyansları eşit olmalı, yani kentteki unutmamış, kırsaldaki unutmuş ise varyans farkı çok olacaktır.
Örnek durum
Niğde Bilsem 7. Sınıf öğrencilerinin Fen Bilimleri dersine yönelik tutumlarının cinsiyet faktörü açısından incelenmesini ele alalım. Bu durumda cinsiyet 2 (kız- erkek) olduğu için bağımsız gruplar t- testi yapacağız. Sayıltılara bakacak olursak bunun için SPSS programında veri girişini “Variable view” kısmında puan ve cinsiyet olarak tanımlıyoruz. Variable View kısmında puan cinsiyet değişkenlerini ayarlıyoruz burada cinsiyet nominal bir veri yani derecelendirmesi olmayan veri anlamına geliyor, puan scale çünkü sayısal bir veri olduğu için bunu seçiyoruz. Daha sonra “Data View” kısmından verilerimizi iki ayrı sütuna giriyoruz.

Öncelikle kaç öğrencinin kız kaç öğrencinin erkek olduğunu anlamak için burada ne yapmamız gerekecek bunu nasıl yapabiliriz ? çünkü bize her zaman az sayıda veri gelmeyecek bazen yüzlerce veri girmemiz gerekebilir ve bu verilere ilişkin sayıları görmek isteyebiliriz bunun için SPSS programında Analyze—> Descriptives statistics—>Frequencies tıklayıp variables kutusuna cinsiyet değişkenini atıp OK diyoruz. Böylelikle toplam kız ve erkek sayısını rahatlıkla görebiliyoruz
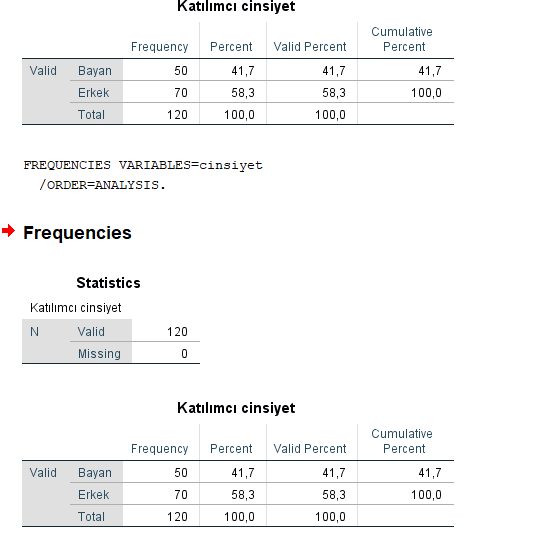
Bilimsel araştırmalarda genellikle yaygın bir anlayış olarak cinsiyetlerin bir birine eşit olması beklenir. bu her zaman her araştırma da eşit olmayabilir, fakat aralarında çok uçuk değerlerde de fark olmaması gerekir. (Sünbül, Ö. 2020/ EPÖ Doktora İstatistik Dersi)
Burada tabloyu yorumlayacak olursak, grup incelediğinde 50’si bayan 70’i erkek olmak üzere toplamda 120 kişiden oluşturmaktadır. Katılımcıların yüzde 41,7 bayanlar yüzde 58 için erkekler oluşturmaktadır.bu durumu grafik ile ifade etmek istersek yine Analyze—> Descriptives statistics—>Frequencies–> Chart kısmını tıklayabiliriz. Burada cinsiyet sınıflama ölçeği olduğu için “Bar” veya “Pie” Chart seçilebilir.

Grafikte oynama yapmak istersek üzerine çift tıklayıp gerekli düzenlemeleri yapabiliriz. Sayıltılarımızda puanların normal dağılım gösterip göstermediğine bakmamız gerektiğini hatırlayalım. Eğer biz 120 kişinin puan dağılımını görmek istersek yine Chart kısmında histogramı seçip normallik eğrisini göster dediğimizde normal dağılım 0lup olmadığını görebiliriz. Ama biz kızların ve erkeklerin nasıl dağılım gösterdiğini ayrı ayrı görmek istersek birkaç farklı yoldan yapabiliriz
Bunun için farklı yollar var;
Birinci olarak data menüsünde Split file kısmını tıklıyoruz burada cinsiyeti seçip “Organize output by groups olan kısmı tıklıyoruz ve Ok diyoruz.
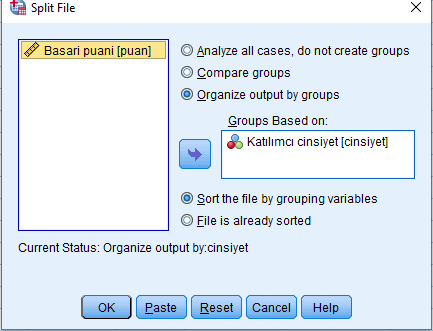
Sonra tekrar Analyze—> Descriptives statistics—>Frequencies deyip Charts kısmında histogramda normal dağılımı göster deyince kadın ve erklerin ayrı ayrı normal dağılımını inceleyebiliyoruz
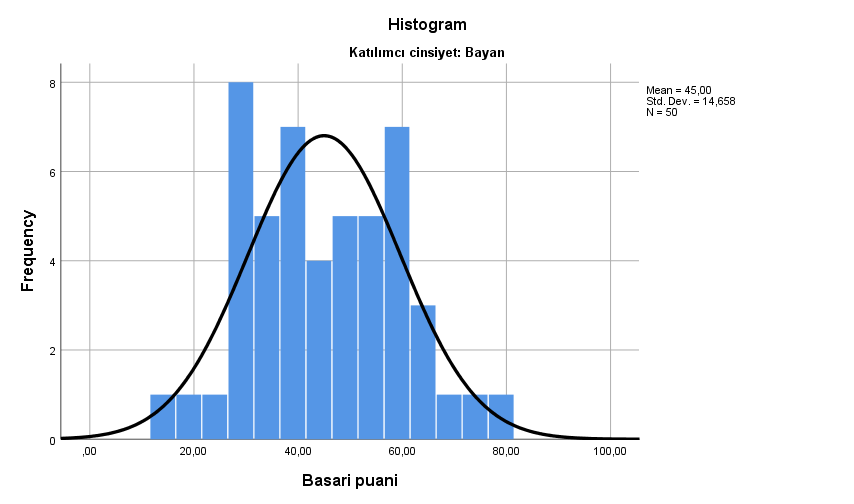
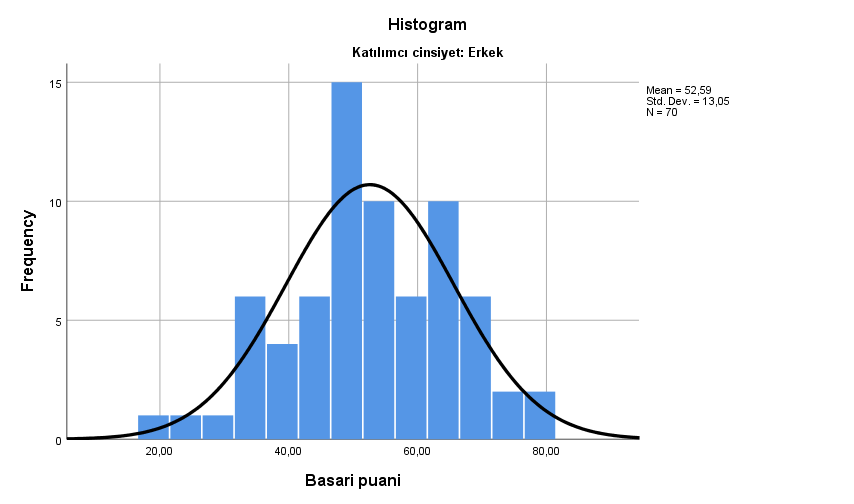
Histogram grafikelri incelendiğinde hem erkeklerin hem de kadınların normal dağılım gösterdiğini söyleyebiliriz
Bir diğer yöntem ise Analyze kısmındaki Explore sekmesinden ise normalliğe bakabiliriz ama bunun için bir önceki Split File işlemini iptal etmeliyiz yani SPSS bütün işlemleri oradaki ayara göre yapacağı için onu iptal etmemiz gerekecektir. Data—>Split File— >Analyze all cases do not create groups aktif ediyoruz ve Split işlemini iptal etmiş oluyoruz.
Daha sonra Analyze—> Descriptives statistics—> Explore tıklıyoruz
Bağımlı değişken kısmına ” puan” , faktör list kısmına ise “cinsiyeti” atıyoruz,. Statistics outlinerleri görrmek istersek tıklıyoruz, Descriptivies de seçildikten sonra , Plots’ dan Normality plots with test’ i seçip , Steam ile başlayanı deaktif ediyoruz ve histogramı tıklıyoruz. Burada tutum puanlarının normal dağılıp dağılmadığını histogram grafiğinde de görmek istiyoruz
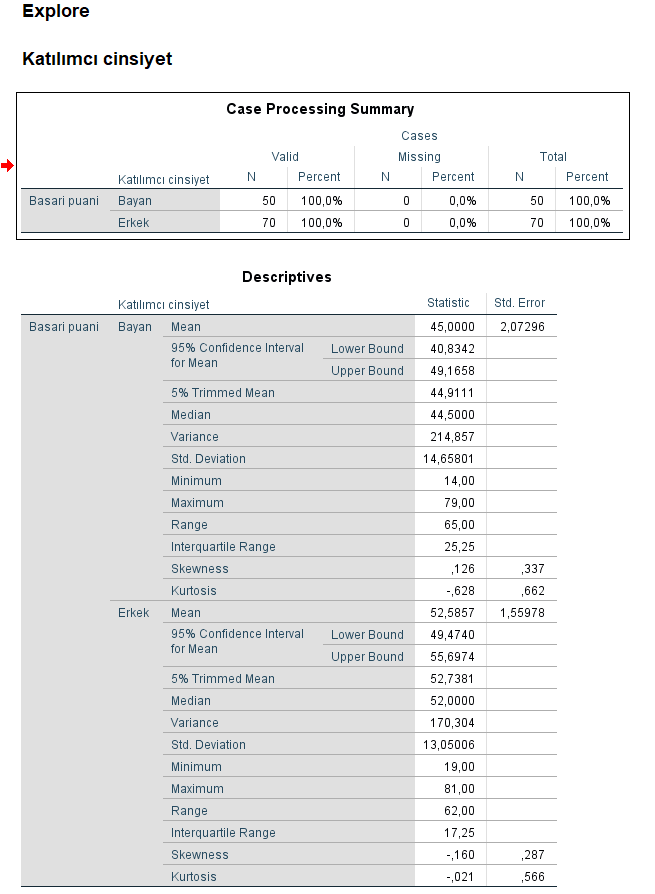
Burada dağılımın normal olup olmadığını anlamak için kırpılmış ortalamalar ile medyan değerlerinin birbirine yakın olması normal dağılım olduğunu gösterir. Başka bir yol ise Skewness çarpıklık ve Kurtosis basıklık değerlerine bakarım bu değerler +1 ile -1 veya +3 ile -3 arasında değerler alması demek normal dağılım olduğunu gösteriyor sıfıra yakın olması çok daha iyi yani normal dağılım gösterme eğiliminde olduğunu bize göstermektedir.

Extrem values da en yüksek puanı alan 5 bireyin puan değerleri ile hangi sırada olduğunu söylüyor bunları görmek istersek buradan bakıyoruz, eğer en yüksek ile en düşüğü atmak istersek yine bu tablodan bakabiliyoruz.
Normallik incelemesinde Kolmogorov- Smirnow ve Shapiro- Wilks değerlerine bakabiliriz. Sig. değeri >. 05 olduğu için bayanları da erkeklerin de aralarında fark yok yani her ikisi de normal dağılım gösteriyor diyebiliriz. Kolmogorov- Smirnowher zaman normal dağılım konusunda bu değerleri vermeyebilir bunun için bu değere bakıp hemen normal dağılım göstermiyor dememeliyiz. Genelde örneklem sayısı 50 den büyükse Kolmogorov- Smirnow küçükse Shapiro- Wilks değerlerine bakılıyor. (Sünbül, Ö. 2020/ EPÖ Doktora İstatistik Dersi)
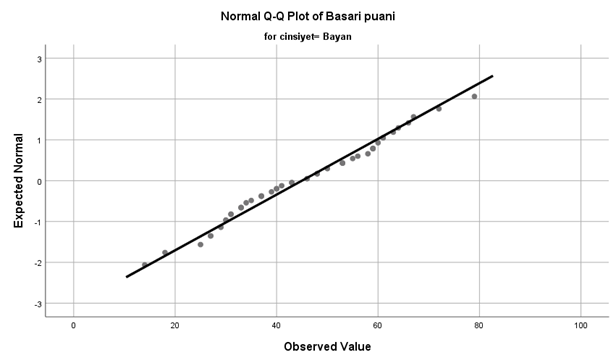
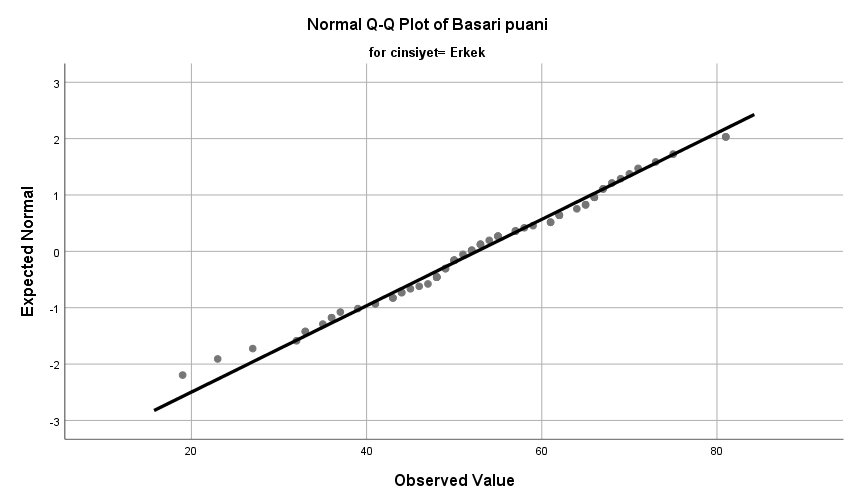
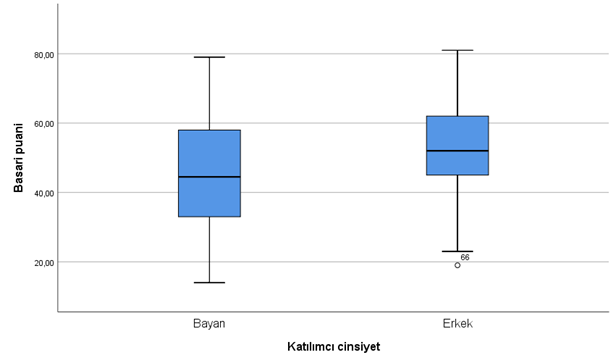
Burada bayan erkek ortalamaları üst ve al puanlar gözüküyor grafik 66′ cı bireye dikkat edin diyor, 66. birey olmasa sileceğiz sonra tekrar normalliğe bakacağız eğer olmazsa normallik o zaman transformasyonlar var Ayrıca varyanslar , standart sapmaları yakınsa normallik sağlanmış oluyor
Tüm bunları kontrol ettikten sonra artık Bağımsız Gruplar T- Testini yapmaya başlayabiliriz
Bunun için Analyze—>Compare Means—> İndependent- samples T-test tıklanır. Burada Test Variable “başarı puanı” Grup Variable ise “cinsiyet” olarak seçildikten sonra gruplar 0 ve 1 diye atanır ve sonra ok denir.
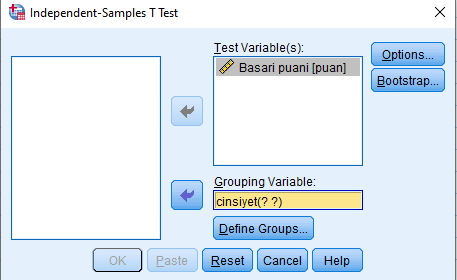
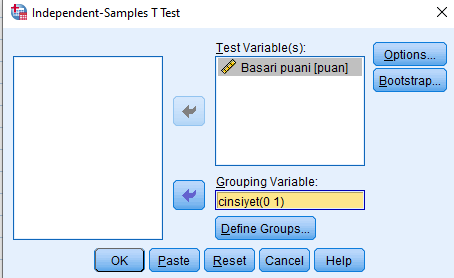
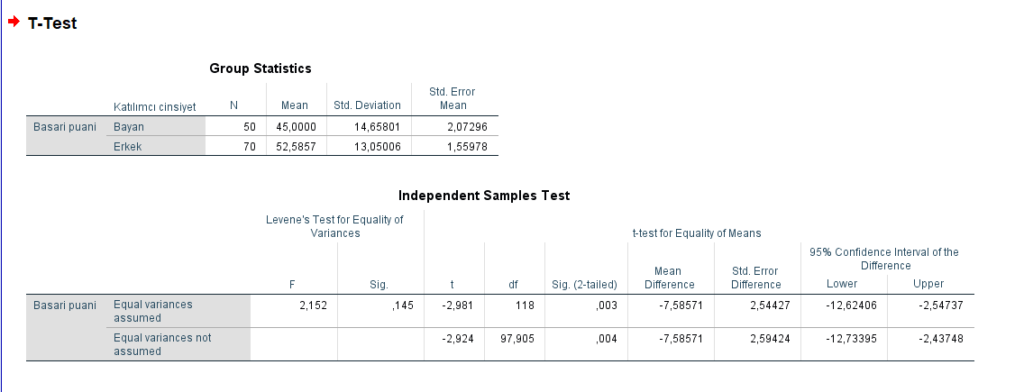
Önce varyanslara bakarsak Levene’s Test for Equality of Variances değerlerinde ikinci satırda Equal variances not assumed olduğu için yukardaki satırdan devam etmek gerektir yani varyanslar .05 den büyük çıkmış varyanslar arasında fark yoktur diyoruz bu durumda bakmamız gereken üst satır burada Sig. (2-tailed) bakarız .003 çıktığı için bunların arasında fark var yani bayanların puan ortalamaları ile bayların puan ortalamaları arasında istatistiksel fark vardır demektir.
Burada kim daha büyük bunu söylemek için üst tabloda ortalamaların 52. 58 erkeklerin lehine olduğunu söyleyebiliriz
